零碎知识点、求最小乘积方案思想、运算符优先级……
NanoApe
posted @ 2016年2月16日 23:03
in 蒟蒻不撕烤智熵何来
, 1147 阅读
曼哈顿距离性质
|x1−x2|+|y1−y2|=max(|(x1+y1)−(x2+y2)|,|(x1−y1)−(x2−y2)|)
扩展到 K 维就各个维正负号都取一遍
求最小乘积方案思想
将每一种方案看作一个点,然后先找到单独考虑每个维的最小解,连在一起即可对应一个线段或平面
然后找到截距最小的解,递归求解即可获得所有下凸包上的方案
其中就可以套各种奇怪的算法(生成树啊背包啊)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | struct P{int x,y;} Ans;bool operator < (P A, P B){return 1LL*A.x*A.y<1LL*B.x*B.y || (1LL*A.x*A.y==1LL*B.x*B.y && A.x<B.x);}void Solve(P A, P B){ P C=FindAns(A.y-B.y, B.x-A.x); if (C<Ans) Ans=C; if (1LL*C.x*(A.y-B.y)+1LL*C.y*(B.x-A.x)>=-(1LL*A.x*B.y-1LL*A.y*B.x)) return; Solve(A,C); Solve(C,B);}int main(){ //.... P A=FindAns(1,0), B=FindAns(0,1); Ans=min(A,B); Solve(A,B); //....} |
运算符优先级
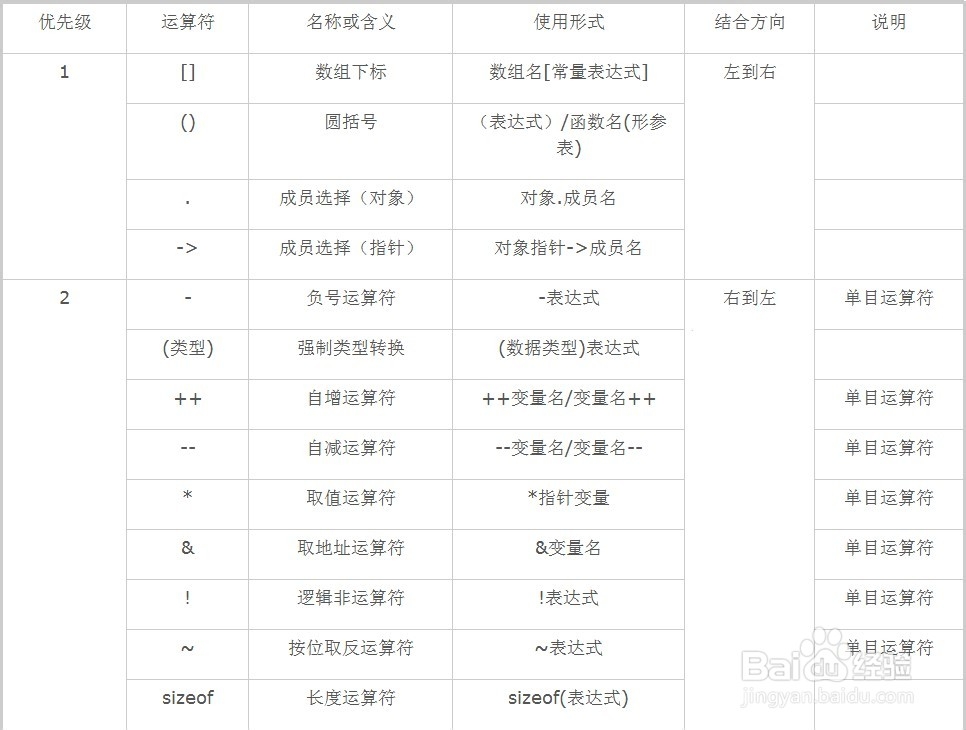
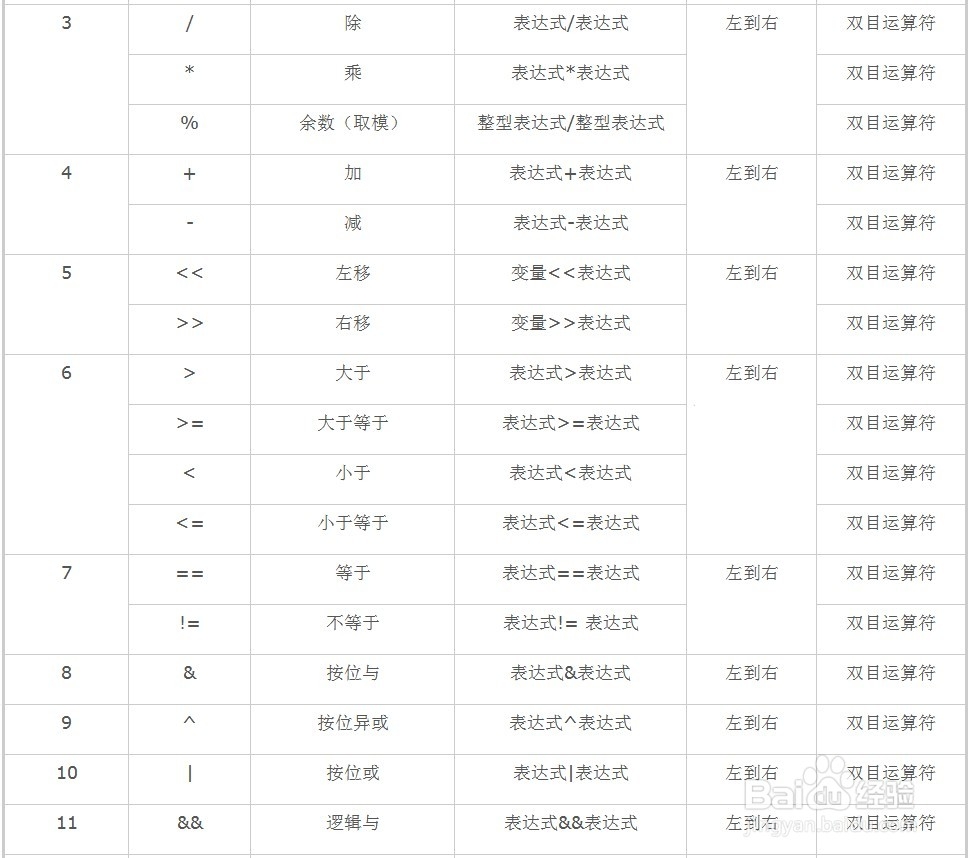
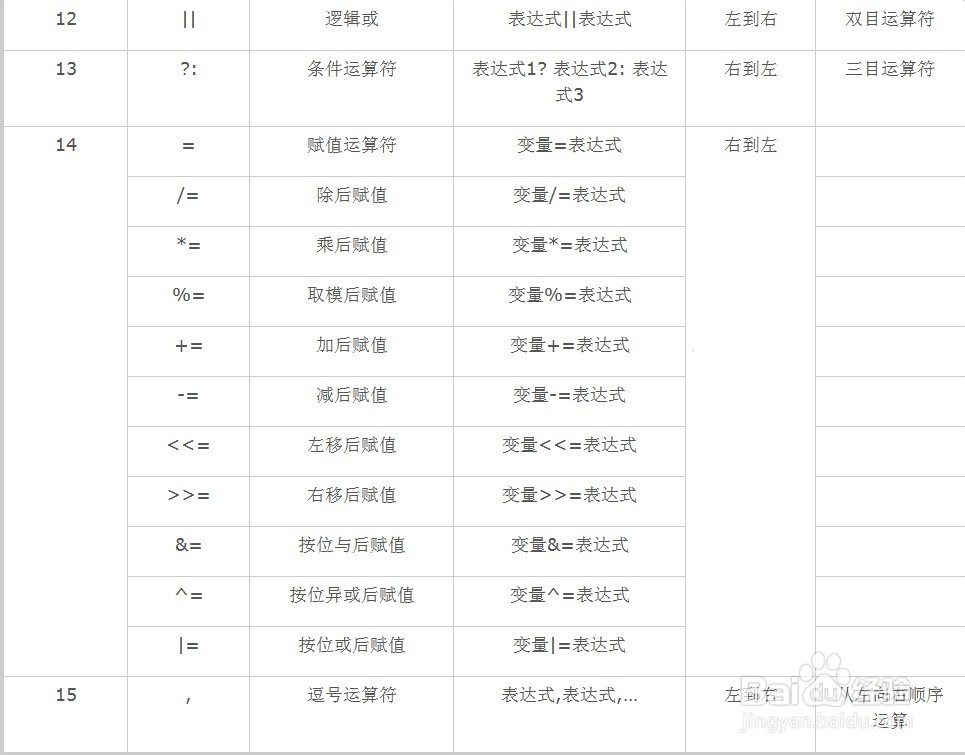
Others
有两个互质数a和b,则最大无法表示成 ax+by 的数是 ab−a−b
三个以内的三角数之和能表示任意自然数
Lindström–Gessel–Viennot 定理
给两个点集 A,B,求不相交道路方案数(强条件为只有一个合法两两对应方案)
方案数为
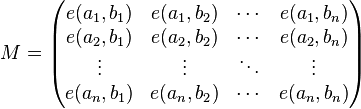
其中 e(a,b) 表示 a 到 b 的路径条数
 评论 (0)
评论 (0)