2015 Contests
Now Solve:25/65
BestCoder Round #44 B
给N个数字,求$\sum lowbit(A~xor~B)$
建立二进制Trie,然后$lowbit(A~xor~B)$等于最小的一个A和B不同的二进制位
BestCoder Round #45 C
求树上路径中出现奇数次的点权,保证只有一个
路径xor一发
BestCoder Round #48 B
给一个图,将点分成两个非空点集,使得点集的导出子图的边数为0
每个联通块二分染色后哪种颜色多选哪种
注意细节:只有二分图有解;只有N>1有解;非空点集;有可能有多个联通块
★BestCoder Round #48 C
给定一个序列,每次询问区间$l-r$,求$\sum ai^{bi}$,其中bi是指ai在区间中的出现次数,ai是指有在区间中出现的数
分块
离散化后预处理出Bcnt[B,k](前B个块中k的出现次数)和Bans[Lb,Rb](第Lb块至第Rb块的答案),然后对于一个询问可以分块根号处理
BestCoder 1st Anniversary C
有一串数列,$Ai=3i(i-1)+1$,然后对于给定的M要从A数列中选取尽量少个数(可重复),使得$\sum Ai=M$
思考,$3i(i-1)+1={6i(i-1)/2}+1$,而$i(i-1)/2$是三角形数,任意一个自然数最多只需要3个三角形数即可表示
所以设m是由k个数组成的,$M=\sum(3i(i-1)+1)=6*(k个三角形数之和)+k$
所以我们分情况来看:假如k=1和2则直接求,$k\le3$时只要$(m-k) \mod 6 = 0$就找到解
BestCoder 1st Anniversary D
给一个二分图,求最多加几条边就能变成完全二分图。不允许有重边。
我们要使二分图两点集的点数差最小。
首先,对于原图中的一个联通块,我们黑白染色,同色的只能分到同一个点集。
然后,DP[i][g]表示前i个联通块能否选取得到大小为g的点集,$n^2$的转移。。。
N多大?10000。Bitset优化。
BestCoder Round #50 (Div.1) C
一段长为n的序列初始时值相同,定义“高平原”为一段值相同且大于左右相邻格的值的连续区间,每次区间加减求位于高平原的格数。
维护相邻两个的差,修改就转化成了两个值的修改,然后高平原肯定是一个正数+一段0+一个负数,最后用动态加点线段树维护一下就行。
BestCoder Round #51 (Div.1) A
求置换的最小循环长度,也就是求最小公倍数
质因数弄出来后求一发就可以了
错误做法:乘积除以gcd
BestCoder Round #51 (Div.1) C
求一个Trie上的回文子串长度和
dfs的时候可持久化回文树搞搞(还能动态查询QwQ
BestCoder Round #52 (Div.1) D
前后加字符,维护回文树
Last变成两个,其余跟普通回文树一样。同时注意假如增加了一个新的结点,两个Last都要维护
BestCoder Round #55 E
有一棵树,每个节点有个权值,特殊之处在于每个叶子节点都是根的父亲,每次询问求节点u到节点v权值和最小的路径的权值和以及这条路径上的权值最大的节点的权值
路径有三种:
一、从u直接到v(链剖)
二、从u(v)到某个叶子,通过叶子到根,再从根到v(u)(树DP)
三、这种情况容易被忽略,就是从u到叶子,通过叶子到根,根再到叶子,然后叶子到v(树DP)
BestCoder Round #58 (Div.1) C
在序列$a_1,a_2,...,a_n$中删除一个长度为m的连续子序列,使得逆序对数最少
枚举删除区间求删除后的减少量,利用预处理+树状数组可以O(1+logn)
BestCoder Round #58 (Div.1) D
给一个图,随机选取边q次,求有多少选取方案使得去重后形成一棵树
通过DP+矩阵快速幂求出一棵生成树的选取方案,对于任意一棵生成树方案数都一样,所以求生成树个数(Kirchhoff矩阵,行列式对合数取模求值)
BestCoder Round #59 (Div.1) B
贪心安排顺序+DP
BestCoder Round #59 (Div.1) C
设01串中最长连续0子序列的长度为A,随机生成01串求A的期望
设$P(x)$为$A<x$的概率,那么$Ans=\sum i[P(i+1)-P(i)]$,每个$P(i)$可以$O(n)$求
★BestCoder Round #62 (Div.1) D
给定一棵树,N个节点,每个节点上有一个字符串。M次询问,每次询问给定两点和字符串S,求两点间路径上字符串为S子串的节点最长长度
先树链剖分,得到dfs序;然后对所有name建立AC自动机。对于自动机上的每一个结点,建立一个可持久化线段树$T(x)=T(fail(x))+w(x)$。T(x)对应的是dfs序,维护的是的maxlen。每一次查询一个串,我们只需要将这个串在自动机经过的点中查询主席树中对应的树剖区间即可。复杂度$O(|S|log^2n)$
BestCoder Round #63 (Div.1) C
有n个球,共有m种颜色,第i个球的颜色为j的概率已知。对于第i种颜色,若有x个球,对答案的贡献为$x^2$。问答案的期望。
突破口:$x^2$的贡献可以看成是两球颜色相同的对数。然后就计算两两球之间颜色相同的概率。
BestCoder Round #63 (Div.1) D
点分治
BestCoder Round #66 (Div.1) B
设$f(x)=\sum_{k=0}^x (-1)^k 2^{2x-2k} C_{2x-k+1}^k,f_0(x)=f(x),f_n(x)=f(f_{n-1}(x))(n \ge 1)$
求$\phi(f_n(x))$
这题假如放在比赛来给你打,就是让你打表找规律。。。
求证:$f_n(x)=n+x+1$
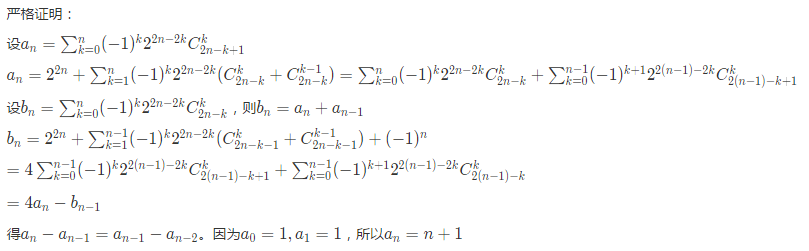
Codeforces VK Cup 2015 - Finals A
给2n个字符串,两两配对使得lcp最大
贪心,在一棵子树上若有两种子串的结尾节点的话就配对,剩余的就扔到父亲集中
Codeforces Round #Pi (Div. 2) E
给一有向图,问某条边有没有可能是最短路网的桥(就是走最短路必须经过这条边),若不是则需要减少多少边值才能满足要求
两边跑个最短路,然后求最短路网内的桥边,再判断需要减少多少边值
STSR #2 B
求$\sum_{x=1}^n\sum_{y=1}^n gcd(x,y)(n\le10^9)$
记忆化搜索$f_k(n)=\sum_{x=1}^n\sum_{y=1}^n [gcd(x,y)=k]$其中有两种性质:$f_k(n)=f_1(n/k)$和$\sum_{i=1}^nf_i(n)=n*n$
STSR #2 C
维护向量集,支持插入和删除向量,以及询问某个向量的点积最大值
对于每次询问可以知道答案一定在凸壳上。以时间为轴建线段树,离线处理所有点存在的时间区间,插入线段树,树上每个点维护凸壳。$O(nlog^2n)$的复杂度
CodeVS 月赛 #1 C
有两棵树,加一条边连接起来形成树S,求S的最短直径和期望直径
预处理出每个点与树中所有点的最远距离,和每棵树的直径长度,然后O(n)扫一遍求最短直径,期望直径就排序后O(n)扫一遍
 评论 (0)
评论 (0)